推文作者： 华中科技大学管理学院 何凡
原文信息： Zacchia P. Knowledge spillovers through networks of scientists. The Review of Economic Studies, 2019.
原文连接： http://www.restud.com/wp-content/uploads/2019/05/MS22668manuscript.pdf
1.引言
知识溢出作为经济学分析的核心理论，已被广泛用于解释产业创新、地理集聚、经济增长和国际贸易等领域相关问题。然而，知识在不同组织间流动的确切机制仍不清楚。经济学家普遍猜测个体互动和空间邻近是驱动信息交换的重要因素，但由于缺乏个体在不同组织交流的微观数据，这一机制长期处在理论分析阶段，缺乏实证支持。本文通过衡量科学家网络关系，考察了个体互动在知识溢出中的作用，为评估研发溢出效应提供证据支持。
作者通过分析专利的合作者识别科学家在不同组织间的联系，并采用组织间交叉联系的科学家比例衡量企业间的关联度。结果发现，以联系强度为权重的关联企业研发投入与企业自己的绩效和创新率显著正相关。然而，这一结论可能只是反映了共同的、未被观察到的混杂因素的影响，如行业技术冲击等。同时，更知名、联系更紧密的科学家可能会被更有生产力、薪酬更高的公司所吸引，导致企业间的关联强度存在内生性。为此，作者构建一个企业间的研发博弈模型，证明了使用距离企业网络较远公司的研发投入作为工具变量的合理性。工具变量回归结果显示，关联企业研发投入确实会促进企业自身的绩效和创新率，在与网络相关的企业中，研发的边际社会回报约为边际私人回报的112%。
2.分析框架
2.1模型建立
一个经济体L表示的N个公司组成，他们的产出不仅依赖资本和劳动力，同时依赖科学家生产的知识资本。将任意两家公司间的联系强度表示为N^2维度集合G={g_ij:i,j=1,…,N}，并且g_ij∈[0, 1]，g_ij=0，说明企业i和j不存在联系。企业层面的知识流网络由集合（L,G）表示，并且网络是无向的，即g_ij=g_ji。
由于公司间正式或非正式的信息交流，一个公司的知识不仅依赖内部研发，还依赖其他关联公司的研发。假设公司i的知识资本S ?_i是其自身研发投资（S_i）和第j个公司研发投资（S_j）的C-D函数，表示如下：
γ∈[0, 1]和 δ∈[0, 1]分别表示内部研发和知识溢出对某企业知识资本的相对贡献，j公司向i公司流动的知识强度取决它们在网络中的链接强度，用溢出权重〖 g〗_ij表示。
知识资本S ?_i作为额外投入进入企业一般生产函数，也是C-D函数形式：
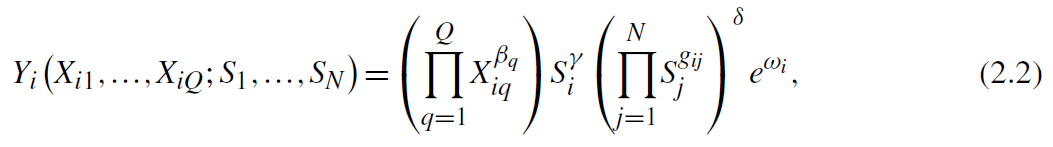
X_iq是常规投入（资本、劳动等），β_q是其弹性参数。产出还取决于随即冲击ω_i∈R，象征其他技术和环境影响公司生产力和盈利能力。R&D成本函数w(S_i,?_i)也依赖网络中空间相关的随机变量?_i∈R：
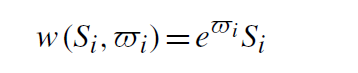
随着?_i值增大，额外研发S_i单位成本也增加。
考虑网络间依赖关系，不同企业技术特征及其成本因素，作者没有明确网络建模形式。相反，作者把G、技术冲击向量ω_i和成本冲击向量?_i视为联合分布F中随机抽取的，从而保持模型一般性。此外，作者对这种分布没有任何限制，只是F反映的网络形成过程或其他决定因素不太可能使具有相似特征的公司在网络空间中相距太远。为此，引入网络中任意两家公司距离概念。d_ij∈N是企业i, j间最小距离，是G的函数。
基于此，假设1认为：
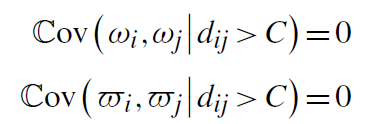
如果i和j间最小路径长度大于C，它们的生产率冲击ω_i和ω_j是相互独立的，它们的成本冲击?_i和?_j也是相互独立的。
通过指定常规投入Q的线性成本参数向量，企业利润函数可以写成：
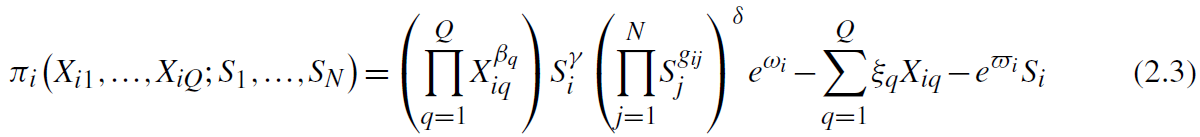
对于任何一家公司，利润既取决于公司特有冲击ω_i和?_i，也取决网络中相关公司研发选择，从而导致企业研发处于均衡状态。因此，任何均衡的概念都应该指明博弈的信息结构。用Ω_i表示企业i观察到冲击ω_i和?_i集合，对该集合结构作了一个相当一般假设：
假设2：每个公司总是观察自己的个别冲击。存在一个整数L，使得单个信息集不包含距离大于L的冲击，即(ω_j "," ?_j )?Ω_i 如果 d_ij>L。
作者将企业最优输入选择问题描述为一个具有时序的不完全信息博弈。通过证明得到存在一个唯一可以表达的贝叶斯-纳什均衡策略轮廓。同时，如果假设1和2成立，可以得到：
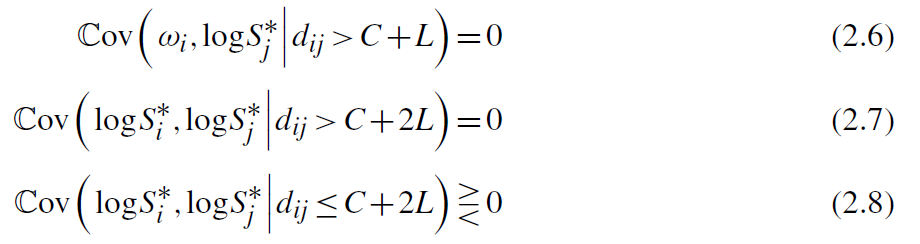
只要一个企业不可观测冲击与另一个企业的均衡研发策略之间距离大于C+L，那么这两个企业的均衡研发策略是独立的；同样，距离大于C+2L的任何两个企业的均衡策略也是独立的，但在距离小于或等于C+2L的情况下都可能是相关的。换言之，对于任何企业i，网络中足够远企业的R&D可以用作距离1处企业R&D的外生预测因子。当前假设没法确保两个关系足够密切公司研发间的协方差（2.8）是非零的，是否能够获得IV有待数据检验。
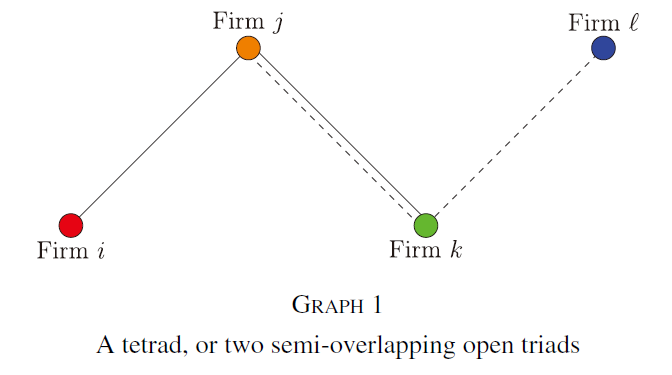
以图1为例，从企业i角度看，企业k的研发可以作为企业j研发的外生预测因子，因为两者是相关的，但前者独立于企业i的研发。然而，l公司研发不是有效预测因子，因为它必然与j公司研发不相关。
3.数据
科学家通常会彼此保持联系，甚至超越他们各自组织的边界。由于职业关系或非正式渠道，公司通过与其他企业有联系的科学家了解其研发活动，研发团队联系越紧密，组织间的溢出效应就越强。为此，企业i和j的联系强度可以表示为：
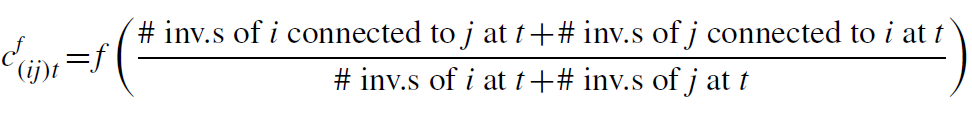
f∈[0,1]，0表示无联系，1表示联系最强。
在应用分析中，我使用基于平方根函数度量关联强度：
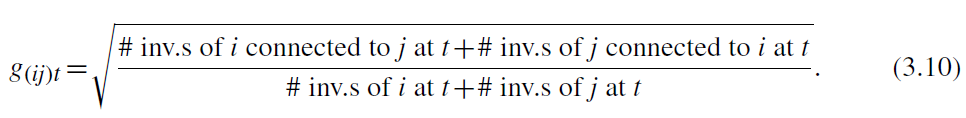
实证分析中，作者将不同的数据集进行合并，最终获得包含1315060项专利的565019名发明者数据，然后计算了每对公司以及1981—2001每一年的关联强度。g(ij)t的均值为0.083，标准差为0.066。解释实证结果的一个有用指标是关联的和，即一个公司在一年内所有关联的总和g ?_it，在关联企业中，g ?_it的均值和标准差分别为0.50和0.57。表1报告了描述性统计结果。
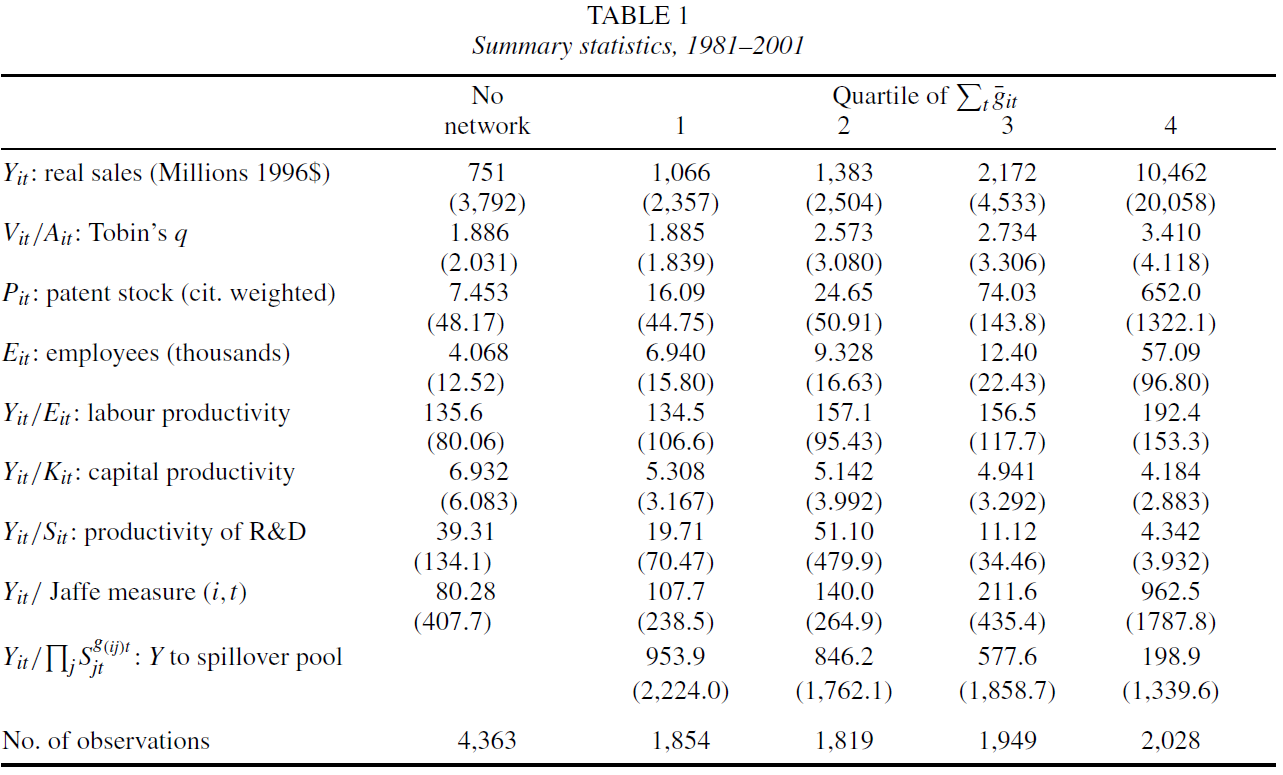
根据实证策略，一组重要的描述性统计值得检验，即网络中企业间R&D的空间相关。图5以Moran’s I数据形式进行了报告，这些数据是针对网络中不同距离企业的研发流量和存量计算的。位于距离2或3处公司的R＆D可能是直接联系公司研发的有效预测指标，只有距离3处的间接链接才能用作适当的预测变量。因此，我使用这两个距离作为IV。
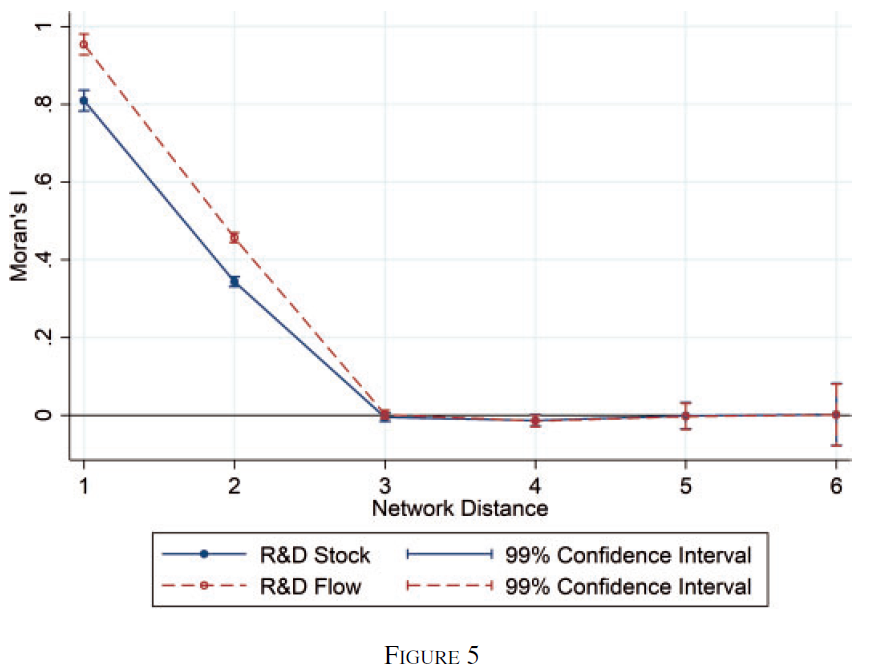
4.计量模型与实证结果
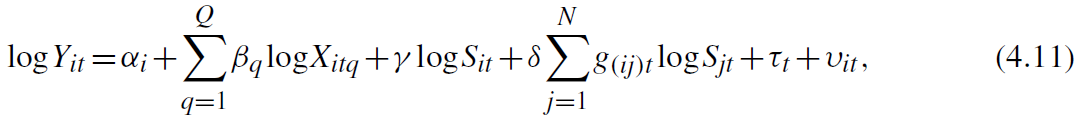Y_it是企业销售额，α_i和τ_t分别是企业FE和时间FE，X_itq是一般投入，S_it是企业自身R&D投入，g(ij)t是关联强度，S_jt是关联企业研发投入。δ是主要关心的系数，被解释为使用关联强度加权的关联企业研发对企业自身生产率的弹性。标准误在网络区域级别进行聚类。正如前文所说，模型存在内生性。为此，作者使用在网络中距离为2或3企业的R&D作为IV。在实际实施方面，作者将所有多个位于距离d的其他公司k的研发投入线性聚合。
表2报告了OLS估计结果，可以发现，在不同样本和控制变量下，δ始终显著为正。以列1为例，关联企业R&D每增加1%，企业自身销售额增加0.008%（0.0159*0.5）。
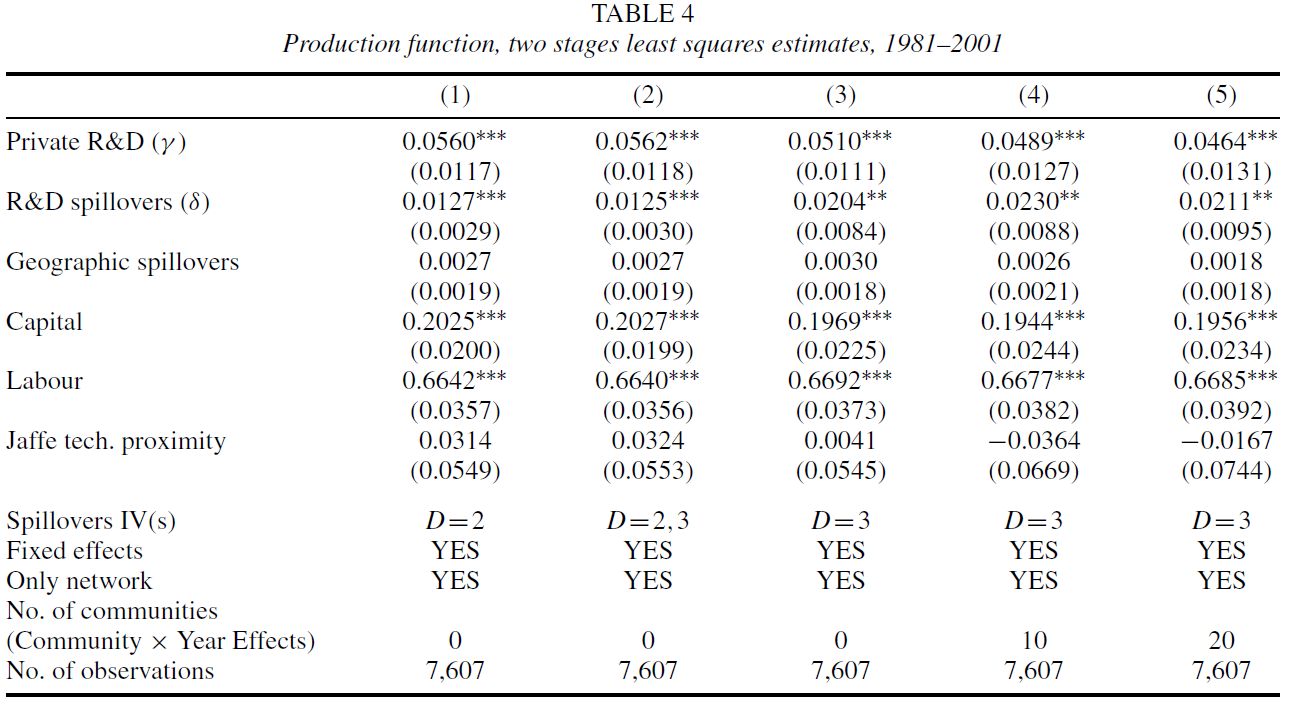
表4报告了IV估计第二阶段结果（第一阶段见原文），δ依然显著为正，但相比OLS估计得到的系数值更大。说明关联企业的研发支出确实会提高企业自身的经营业绩。
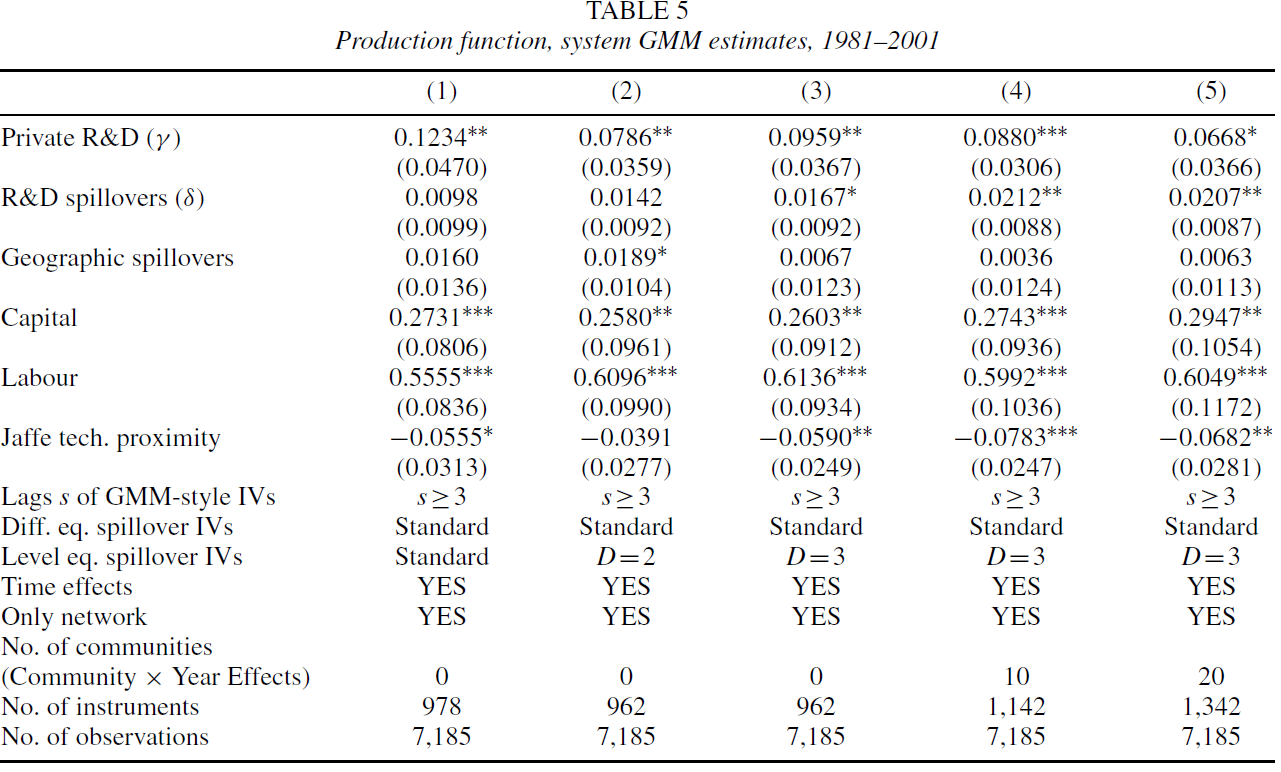
一个可能的担忧是，由于私人投入变量（资本、劳动力、私人研发）也是内生的，相应的弹性可能被错误的估计。尽管模型分析中已经表明使用工具变量可以克服这一问题，但为进一步验证本文结论，在此进行系统GMM估计。表5结果显示，δ值与IV估计非常接近，再次验证了本文结论。
4.结论
通过采用科学家在不同公司的连接强度衡量企业间的关联度，本文评估了研发的溢出效应。在解决内生性问题之后，作者发现，关联企业的研发对企业自身会产生相当大的溢出效应，在与网络相关的企业中，研发的边际社会回报约为边际私人回报的112%。
推荐理由：
知识溢出是解释集聚、创新和区域经济增长的重要概念，大量文献分析了中国国有企业、集团化经营、外商直接投资和工业产业园的知识溢出效应。然而，正如本文所言，以往研究大多使用加总层面的指标进行分析，缺乏个体微观层面数据，导致无法分析知识溢出的内在机制。随着国内发明家数据的使用，从个体层面分析知识溢出的机制与后果成为可能，而本文使用的方法和分析框架无疑能够为我们探讨中国情境下的知识溢出提供思路借鉴。