一、引言
  在预测税制改革的政策效果时,关于税率的应税收入弹性(Elasticity of Taxable Income)是政策制定者十分关心的一个参数。然而,几十年来,尽管大量研究者都投身于估计应税收入弹性,但始终无法估计出一个较为统一的数值,对于弹性的大小依旧存在诸多争议。
  本文研究表明,在个体偏好分布函数没有得到限定时,聚束量无法为估计应税收入弹性大小提供有用的信息。因为拐点或缺口处概率的大小不仅会因应税收入弹性的大小改变而变化,也会随着个人偏好的变化而变化,使研究者无法用单一预算集区分应税收入弹性和个体偏好分布的影响。即使拐点所处的范围较小也无法解决这个问题,因为无论拐点所处的范围是大还是小,都可以通过某一方式改变偏好分布,使得应税收入分布与任何弹性数值相匹配。本文也指出,这种无法识别的问题可以理解为识别条件的缺失,即已知的方程个数需要与未知的结构参数的数量一致。在给定拐点处的收入分布的情况下,我们只得到一个弹性与偏好分布的关系等式,无法同时计算出弹性和偏好分布。
  由此,本文指出,当对个体偏好分布函数加以限定后,拐点就可以为估计弹性大小提供有效的信息。同时,也可以通过设定偏好密度的界限估计出应税收入弹性的界限。作者使用Saez(2010)的数据进行实证检验发现,应税收入弹性大小对偏好分布的界限十分敏感。
  相较以往文献,本文的边际贡献主要体现在以下三个方面。第一,通过严谨的数理证明过程,指出以往研究者使用聚束方法对应税收入弹性的估计有误。第二,首次证明只有在限定个体偏好分布的情况下才可以估计应税收入弹性,为研究者估计弹性提供借鉴。第三,在放松对个体偏好分布函数的限定的情况下,通过限定个体偏好分布函数的性质,估计出了应税收入弹性的边界,为政策制定者提供了参考。
二、应税收入弹性无法识别的原因
  本文首先设定个体效用函数是消费、收入和个体偏好的函数,其中c表示消费,y表示税前收入,η表示不可观察的个体偏好异质性,即U(c,y,η)。
  图2展示了税率在K点发生变化时,预算线的变动以及效用最大化时的应税收入选择。图2的横轴表示收入,纵轴表示消费,粗实线表示实际预算线,浅实线表示反事实的预算线,虚线都表示无差异曲线,由于在K点应税收入的税率发生了变化,因此实际预算线的斜率发生了变化,在K点处出现一个拐点。如果在K点处税率没有上升,那么预算线的反事实情况就如图2中的浅实线所示,在效用最大化时个体会选择K+∆Y点处的应税收入。然而,由于在K点处税率上升,所以在K点后预算线的斜率下降,收入的最优选择在K点处。因此,税率的变化导致个体收入选择从K+∆Y变成K,其中∆Y点是收入的变动量,实际预算线的斜率的变动就反应了税率的变化。因此就有(1)式的应税收入弹性公式,其中,ρ1、ρ2分别表示实际预算线在K点之前、之后的斜率。
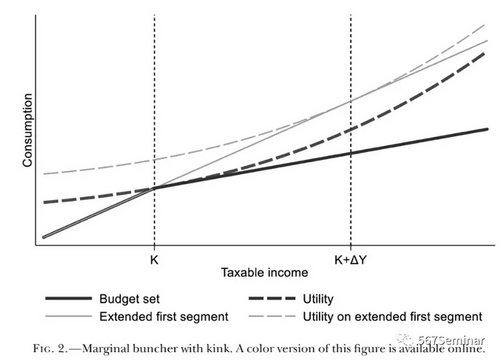

  图2也表明,在K点处税率未发生变化时,有许多个体分布在K至K+∆Y处,而税率上升后,由于追求效用最大化,K至K+∆Y处的个体将聚束至K点处,本文用(2)式表示K点的聚束量

  在求得弹性的基本公式以及聚束量的积分公式后,为了简化计算过程,专注于弹性的估计问题,本文参照Saez(2010)的做法,将效用函数设定为等弹性效用函数,如(3)式所示:
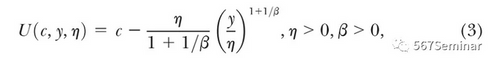
  在已知效用函数的情况下,结合预算线的约束情况,通过效用最大化条件,就可以求得收入、偏好与预算线斜率的等式。由此可以得知,β就是不变的应税收入弹性。

  通过收入、偏好等式,结合(2)式,本文就得出聚束量与偏好概率密度函数的积分公式,如(4)所示:
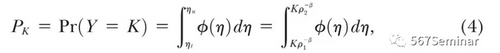
  据此,本文也提出了理论1,即假定应税收入的分布函数在K点左右都是连续的且大于零,偏好密度函数在K点左右也是有差异的。那么对于任意的应税收入弹性,都存在一个偏好的密度函数与之相匹配从而满足等式(4)。这就说明了,在这一个等式中,如果不对偏好密度函数加以限定,那么就无法求得一个确切的弹性值。
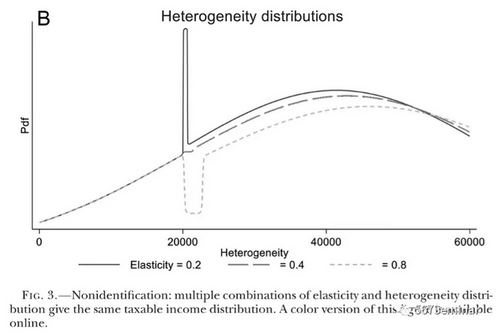
  为了让读者更直观地理解理论1的内容,本文还通过图3展示了不同应税收入弹性时的偏好密度函数形式。其中,实线表示弹性为0.2时的偏好密度函数形式,长虚线表示弹性为0.4时的偏好密度函数形式,短虚线表示弹性为0.8时的偏好密度函数形式。从图中可以看出,在K点附近,弹性值与偏好密度函数成反比,即更大的弹性与之相匹配的是更小的偏好密度函数。
  聚束效应(Bunching)不仅有拐点(Kink)形式的,还有断点(Notch)形式的。在前面部分,本文主要讨论的是拐点形式的聚束效应,而在此处进一步讨论了在断点处的弹性是否也无法估计。图4中横轴表示收入,纵轴表示消费,实线表示预算线,虚线表示无差异曲线。在K点处表示平均税率发生变化时的情况,即平均税率上升后,在同等收入水平下,个体所能消费的额度将下降。因此在K点处出现一个断点。在K点之前的这段预算线,个体效用最大化的点在K值处,而当平均税率上升后,预算线斜率下降,效用最大化点yg(β)处的效用与K值的效用相等,且在K与yg(β)处的点的效用低于K值处的效用,因此分布在K与yg(β)之间的个体将会调整自身的收入水平,让自己分布在效用更大的K点处。
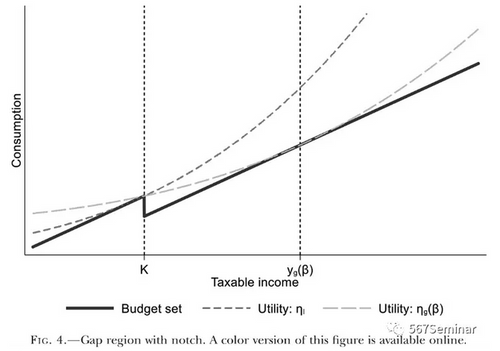
  由上图分析,本文指出在断点(Notch)形式中收入的变化是从yg(β)至K。结合式(4)可得Notch的聚束量等式,如(5)式所示:

  以往研究者,例如Saez(2010)和Chetty(2011),之所以能够估计应税收入弹性,就在于他们都限定了K点附近的偏好分布函数形式。Saez(2010)就假定在[ηl,ηu]区间内,偏好密度函数是线性的,由此可以推导得(6)式:
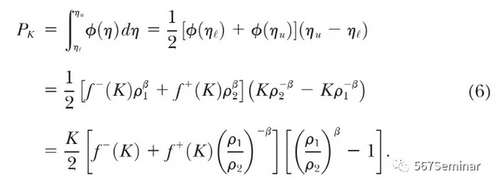
  通过(6)式就可以求得应税收入弹性。
三、单拐点预算线的应税收入弹性边界
  在图3中本文就指出,在给定拐点处的聚束概率后,当弹性较大时,聚束区间内的偏好密度函数就较小;当弹性较小时,聚束区间内的偏好密度函数就较大。弹性和偏好密度函数的这种关系也说明了,在聚束区间内,可以通过偏好密度函数的边界估计应税收入弹性的边界。
  在估计弹性边界时,本文指出如果在排除区间(excluded range)内取拐点的边界,那么就会导致最优误差。为了减少最优误差对估计结果的影响,本文在排除区间(excluded range)外取拐点的边界(y1,y2),且y1
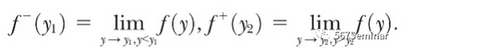
  由此可得弹性的分布函数:
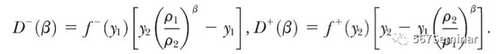

  通过理论2的定义,并结合弹性分布函数,可得(9)式,由此求得弹性的上下界:
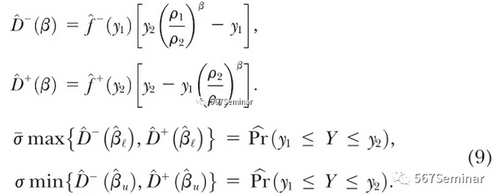
四、利用美国数据估计应税收入弹性边界
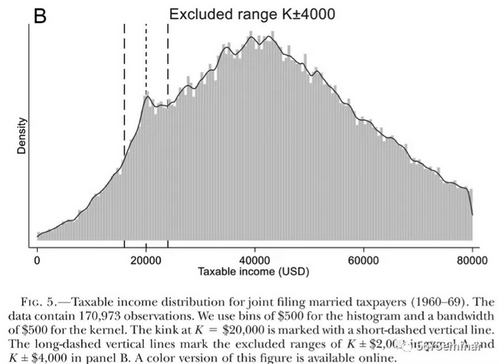
  在说明如何求出弹性边界后,本文期望利用美国数据估计应税收入弹性边界,并与以往研究者的估计结果进行对比,以此验证此方法的正确性。本文参照Saez(2010)的做法,使用1960年至1969年的个人公共使用微观数据(Individual Public Use Microdata)研究针对已婚联合纳税人的联邦所得税政策,即当已婚联合纳税人的收入不超过20000美元时,税率为零,而当已婚联合纳税人的收入超过20000美元时,边际税率将上升至16%。在图5中,作者将排除范围(excluded range)设置为K值左右4000美元的范围,图中可以明显看出在20000美元处存在显著的聚束效应。
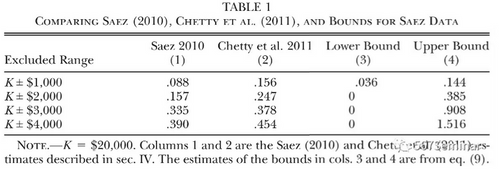
  基于前部分的推导结果,本文使用前面的计算公式估计出了应税收入弹性的边界,如表1所示。表1最左侧一列是排除区间取不同的范围,第(1)列是参照Saez(2010)的做法将偏好密度函数假定为线性后的估计结果,第(2)列是参照Chetty(2011)的做法将偏好密度函数假定为多项式后的估计结果,第(3)列是使用本文的估计方法得出的应税收入弹性的下界,第(4)列是使用本文的估计方法得出的应税收入弹性的上界。由此,本文在放松对偏好密度函数的限定的情况下,成功估计了应税收入弹性的边界。
推荐理由:
  应税收入弹性对于提前预知税收政策的影响至关重要。虽然已有的聚束方法能够估计这一弹性,但本文研究表明,在个体偏好分布不受限制的情况下,聚束方法也无法准确估计弹性大小。本文另辟蹊径,基于偏好密度的边界从而估计出了弹性的上下界。这篇文章对聚束方法的研究不仅能够提醒众多研究者在使用实证方法时,要时刻关注实证策略的适用条件,不可盲目照搬套用。而且本文估计弹性的方法也可以用于估计我国税制改革的政策影响,为我国政策制定者提供有效的预测参数。
