一、引言
  高科技集群对城市和一国的经济增长具有重要意义。根据以往研究,高科技产业具有较强的地理集聚倾向,比如西雅图的互联网和软件集群、波士顿的医学和生物技术集群、奥斯汀的软件和电信集群等。有趣的是,尽管高科技产业集聚地区的劳动力成本和生活成本都比较高,但发明者仍然出现集聚现象。这种集聚会对顶尖发明家的生产率产生影响吗?由于高科技集群的地点是内生的,企业和劳动力区位决策的影响因素较为复杂,如果生产率高的发明者选择进入大集群,那么不同规模的集群对发明者生产率影响的估计会产生偏差。
  本文使用1971-2007年美国顶尖发明家专利申请的纵向数据,研究以下两个问题:(1)高科技集群能否提升发明家生产率?(2)地理集聚对美国整体创新的总效应是什么?首先,作者通过对罗彻斯特集群进行案例分析发现,柯达公司的衰落导致罗彻斯特集群规模锐减,发明者的生产率大幅下降。其次,作者通过对全样本进行分析发现,一个发明者从小规模集群迁移至大规模集群时,其生产率显著提高。最后,作者通过相对于集群规模的生产率弹性估计发现,高科技集群会显著提高美国专利总量。
  二、数据介绍
  本研究使用的专利数据来源于COMETS数据库。
  2.1专利、发明家与其位置
  首先,数据包括4229809项专利。其中,受雇于私人公司的发明者申请专利占比为90.9%。其次,本文使用的地理分析单位是美国经济分析局(BEA)的179个-经济区-(作者称为城市),每一项专利都根据发明者的居住地址分配到一个经济区。最后,在COMETS数据中,专利被分配到五个主要研究领域和579个技术类别。
  本文将集群定义为城市和研究领域的组合,共有179个城市和5个研究领域。另外,本文通过集群中发明者的数量衡量集群规模。
  2.2数据局限
  本研究使用的数据存在两个局限。首先,作者认为使用专利数量衡量发明者的生产率并不完美。虽然有些专利代表了某个领域内的创新,但也存在基于防御目的而申请的专利。同时,有些创新没有申请专利,获得专利的创新比例也因研究领域和技术层次的不同而不同。为弥补这一缺陷,本研究使用专利引用次数衡量专利质量。第二个局限源于样本选择,发明者并非每年都申请专利,因此,作者不能准确识别每个发明者每年的生产率和位置。为解决这一问题,作者将明星发明家作为主要研究对象。
  三、柯达破产对罗彻斯特高科技集群发明者的影响
  本文中,作者以柯达公司为例,实证检验了在数码摄影技术推广这一外生冲击下,柯达公司的衰落导致罗彻斯特高科技集群规模缩小是否对非柯达发明者的生产率产生影响。图3显示了1990-2007年间罗切斯特非柯达发明家平均生产率的变化,在1996年数码摄影技术推广之前,对数平均生产率保持持平,但1996年之后,对数平均生产率开始下降。此外,作者还进行了双重差分估计,比较了1996-2007年间罗彻斯特非柯达发明者与其他城市非柯达发明者生产率的变化,结果表明,1996-2007年间,罗切斯特的非柯达发明者的生产率相对于其他城市的发明者下降了20.6%。
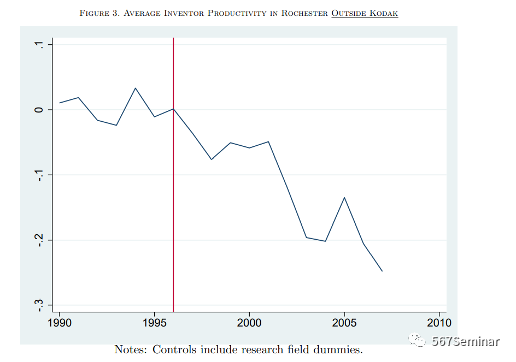
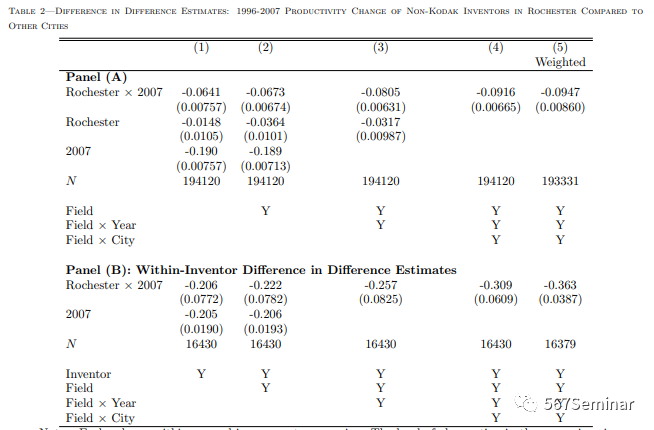
  3.1基准回归
  该部分通过考察样本内所有城市高科技集群规模对发明者生产率的影响,以检验案例分析结果。基准回归模型如下:
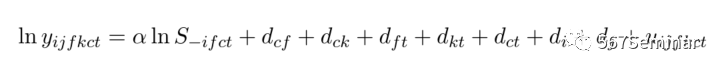
  其中,y为发明者生产率、S为集群规模、i为发明者、j为公司、f为研究领域、k为技术类别、c为城市、t为年份、d为固定效应。基准回归结果如表3所示。
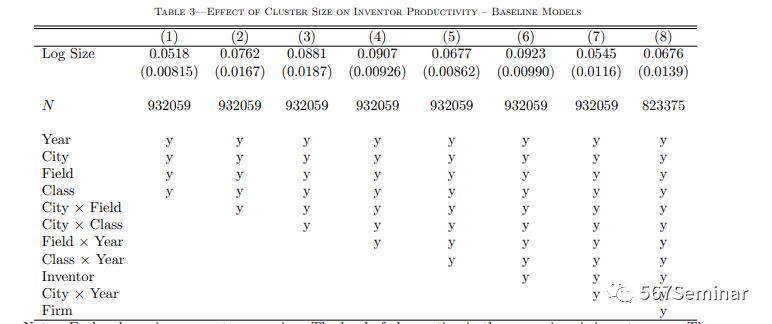
  表3中第8列估计了生产率相对于集群规模的弹性,可以看出,集群规模每增加10%,发明家所产出的专利数量就会增加0.67%。
  3.2动态效应
  基准估计分析了样本中所有高科技集群规模变化对发明者生产率的影响,由于内生劳动力素质和内生劳动力数量两个识别问题,基准估计不能解释二者之间的因果关系。劳动力内生素质(Sorting)是指发明者根据收入、生活成本、当地的公共设施和对特定地点的特殊偏好选择集群。内生劳动力数量(Simultaneity)是指在城市和研究领域层面上存在无法观察到的时变生产率冲击,从而吸引更多的发明家到该城市从事此类研究。基于此,本文在基准回归的基础上进一步估计了集群规模变化后生产率的动态效应。模型如下:
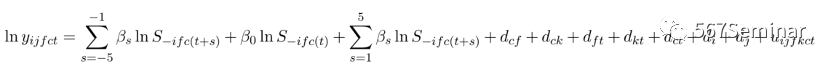
  其中,系数β1至β5表示发明家的生产率对未来5年集群规模变化的响应,系数β-1至β-5表示发明者的生产率对过去5年集群规模变化的响应。动态响应结果如图5、图6所示:
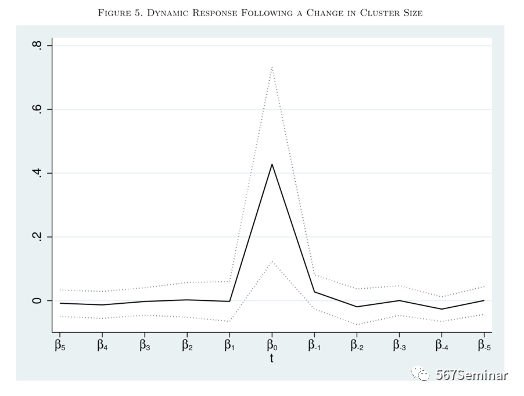
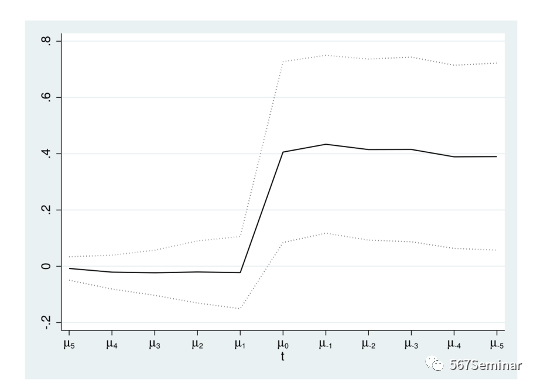
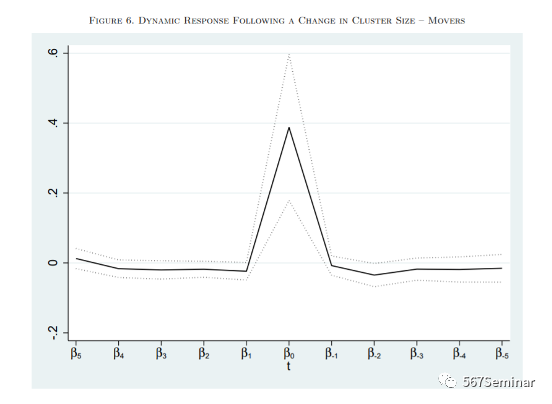

  图5的结果表明未来集群规模的变化对当前生产率的影响,排除了明星发明家从小规模集群迁移到大规模集群对结果的影响,这种对发明者生产率的影响在集群规模变化当年就已有显现。而且,与图5相比,图6非当年生产率下降更多,这表明由发明家迁移带来的影响至少能够持续5年。
  本研究中,作者使用工具变量以克服由内生劳动力数量(Simultaneity)造成的内生性问题。本文首先将其他城市的企业拥有发明者数量作为工具变量,对柯达案例进行2SLS回归,结果如表4所示。
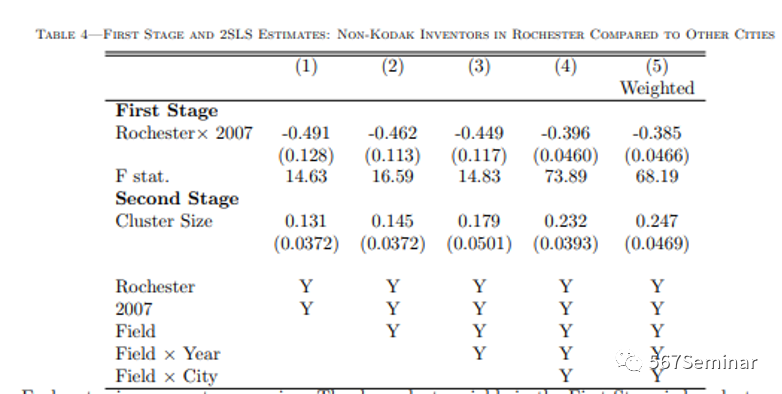
  第一阶段回归结果中,第1列的-0.491(.128)至第4列的-0.396(.0460)表示未加权估计范围,在研究领域和年份、研究领域和城市两个组合中,罗彻斯特的集群规模相对于其他城市下降了39.6%。第二阶段回归结果中,第1列的0.131(0.037)至第4列的0.232(.0393)表示发明者生产率相对于集群规模变化的弹性。
  此外,作者还使用公司空间网络构建工具变量以分离来自其他地区的本地集群规模变化产生的影响。工具变量衡量与模型如下:
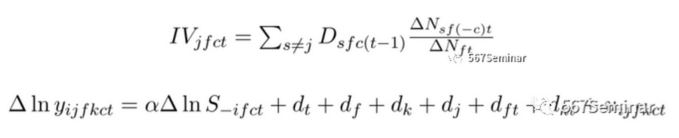
  其中,Dsfc(t-1)表示t-1年该公司在c市f研究领域至少有1个发明者,ΔNft表示该研究领域全美发明家数量的变化。OLS回归和2SLS回归结果如表5所示:
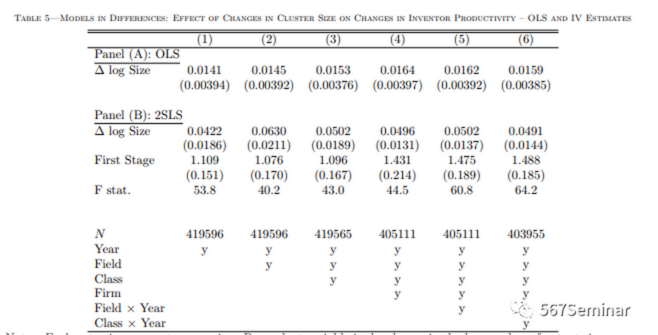
  Panel(A)反应了OLS回归结果,该OLS估计范围在0.0141(0.00394)至0.0164(0.00397)之间,相较于基准回归,水平较低,这一差异取决于固定效应。Panel(B)反应了2SLS回归结果,2SLS估计范围从0.0422(0.0186)至0.0630(0.0211),第6列为0.0491(0.0144)。由于修正了模型中的测量误差和内生性,相较于基准模型,该结果更为显著。
  四、专利引用与异质性分析
  4.1专利接受与引用
  为了更好了解集群规模变化对发明者专利质量的影响,作者将研究聚焦于专利引用次数,即使用专利引用次数衡量专利质量。结果如表6所示。
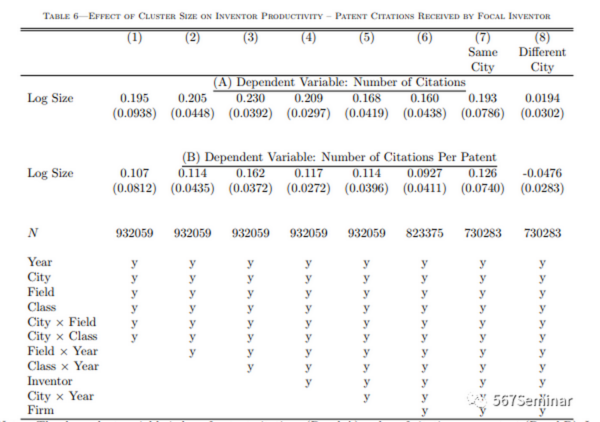
  表6中第6列的估计表明,被引用总数和每项专利被引次数的弹性分别为0.160(0.043)和0.092(0.041)。这意味着,与较小集群中的类似发明者相比,较大集群中的发明者不仅能产生更多的专利,而且其专利影响力更强。第7列和第8列表明,专利引用数量的增加很大程度上取决于本地引用。
  为了阐明科学家在规模较大的集群中生产率会提高的作用机制,作者转向对明星发明家的引用进行分析。结果如表7所示。
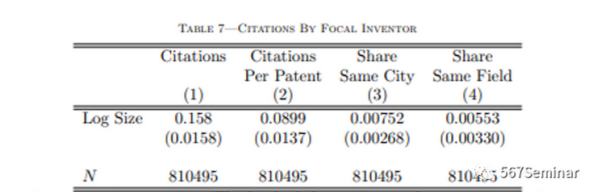
  表7表明规模较大集群中的明星发明家往往比规模较小集群中的明星发明家引用更多专利。
  4.2异质性分析
  作者从集群规模、公司生产率和发明者生产率三方面进行异质性分析,结果如图8、图9所示。
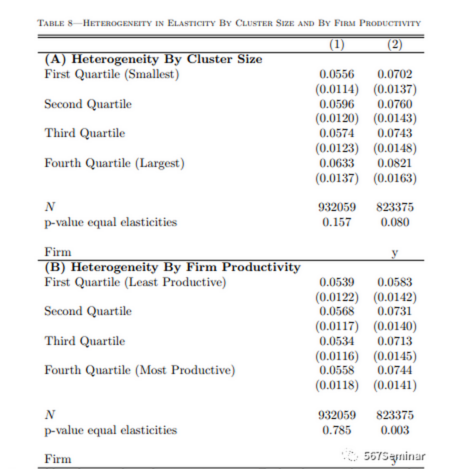
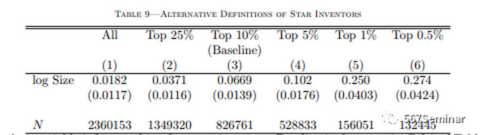
  通过异质性分析,作者得出以下三个结论:(1)在弹性方面存在较大异质性的证据有限;(2)溢出效应作为企业生产率的函数存在差异,但这种差异在经济上很小;(3)生产率高的发明者是集群中最大的受益者,这也反应了发明家质量和集群规模之间的互补。
  五、集群对美国创新总产出的影响
  5.1空间集聚如何影响专利总量
  首先,本研究假定存在A、B两个集群,且集群A的规模大于集群B,即SA>SB。其次,假设发明者i的产出是关于集群规模的函数,即Sc:yic=g(Sc)且g’c>0。在该模型中,经济总产出应是集群A和B的产出之和:
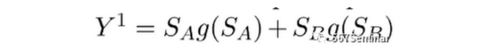
  研究考虑了集群规模均等化这一反事实,即发明者从集群A迁移至集群B,从而使两个集群发明者数量相等。此时,该经济体中的发明者总数不变,但集群A发明者数量减少,集群B发明者数量增加。反事实情况的专利总产出为:
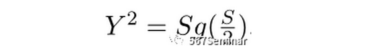
  这种规模变化对总产出的影响为:
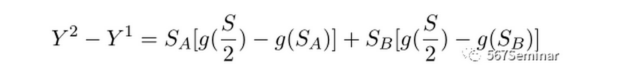
  其中,由于集群A规模缩小了,gongshi ;集群B规模变大了,gongshi 。由上述公式可知,总效应取决于初始集群规模加权的每个集群中发明者生产率的变化。
  本研究进一步将模型扩展至全美所有集群,公式如下:
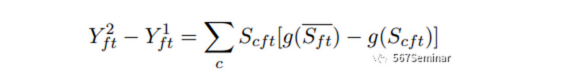
  5.2集聚效应对专利总量影响的估计
  该部分中,作者估算了不同研究领域中发明者生产率对集群规模的弹性,并分析全美集群产生的宏观经济效应。结果如表10、表11所示。
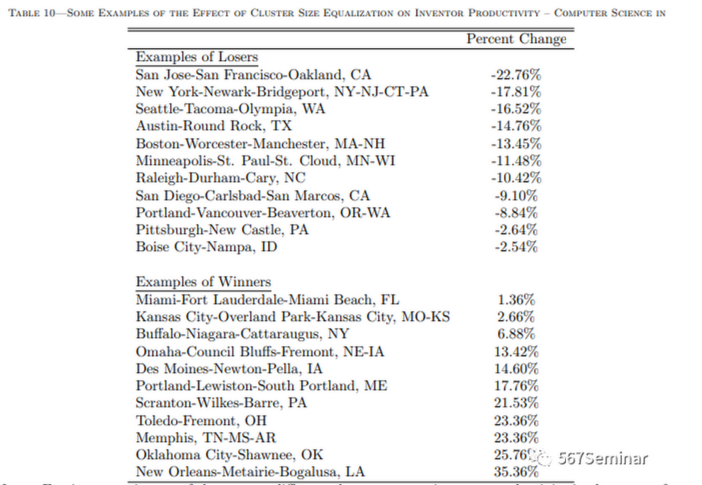
  表10报告了2007年计算机科学领域中集群规模均等对平均发明者生产率的估计效应,从表中可以看出,在集群规模均等的情况下,规模较大的集群生产率会下降。
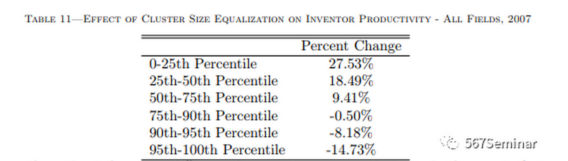
  表11报告了根据初始集群规模估计的规模均等对2007年所有领域发明者生产率的影响。从表中可以看出,大型集群中每个发明者的生产率下降,而小型集群则相反。
  利用上述扩展模型,作者估计了每个研究领域中集群规模均等对美国在该领域产生专利总数的总效应。结果如表12所示。
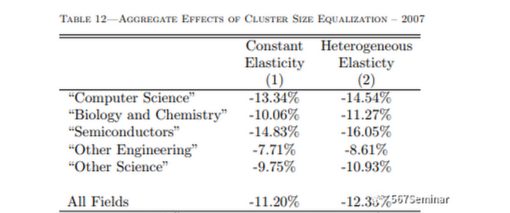
  表12第1列对2007年5个研究领域的总效应进行估计。如果5个领域的发明者均匀分布在各个城市,那么2007年美国计算机科学领域的专利总量将会减少13.34%,生物与化学领域、半导体领域以及其他工程和科学领域分别会减少10.06%、14.83%、7.71%和9.75%。
  六、结论
  本文通过实证分析发现集群规模对发明者生产率具有重要的经济影响。当发明者从一个小规模的集群转移到一个大规模的集群中时,其生产率会提高,每年产生的专利数量相对于集群规模的弹性为0.0676。此外,发明者的聚集给美国带来经济效益,相较于集群规模均等这一反事实,集群聚集在较少几个地区会使美国某一年专利总量增加11.20%。
  推荐理由:
  -硅谷式集群-对创新的影响是创新领域的经典话题。已有研究表明,高科技产业是当地经济增长的重要驱动力,因此,高科技产业聚集具有重要的经济意义。本文以专利数据量化生产率,并使用专利引用次数刻画专利质量,克服了以往研究中存在的内生性问题,验证了集群规模变化对生产率的影响。此外,通过利用生产率对集群规模的弹性估算全美集群产生的宏观经济效应,本文发现,高科技集群在少数地区大规模集聚才能提升总体创新水平,高科技产业的空间集聚可能会加剧区域间不平等。因此,如何通过产业政策合理调整集群规模及产业结构,缩小区域差距应是未来研究方向。此外,本文也为地区产业政策的制定提供理论基础和现实依据。
